1-4 The Compton Effect
the particle التجربة التي تؤكد بوضوح الطبيعة الجسيمية للإشعاع
تسمى بتأثير (ظاهرة) كومبتون نسبة للعالم كومبتون nature of radiation
لقد اكتشف كومبتون أنه إذا اخترق إشعاع ذو طول Arthur H. Compton
scattered شريحة معدنية فسيتبعثر (X-ray موجي (في منطقة الأشعة السينية
بطريقة لا يمكن تفسيرها حسب النظرية التقليدية للإشعاع.
المنبعث من I الذي تخبرنا به قوانين الفيزياء التقليدية أن شدة الإشعاع
مادة نتيجة تأثرها بإشعاع سقط عليها (مما يؤدي إلى اهتزاز إلكتروناتها والتي
بالنسبة لاتجاه الأشعة ) θ بدورها ستبعث إشعاع) عندما تقاس عند زاوية
حسب العلاقة θ تتغير مع I الساقطة) فإن
PDF created with pdfFactory Pro trial version www.pdffactory.com
- ١٨ -
Ι » (1+cos2θ) (1-
لا تعتمد على الطول الموجي للأشعة الساقطة، وهذا I وهذا يعني أن
I 1) والتي يتبين بوضوح تغير - يتعارض بوضوح مع النتائج التجريبية (شكل 6
.l بتغير
Figure 1-6. The spectrum of radiation scattered by carbon,
showing the unmodified line at 0.7078 Å on the left and the shifted
line at 0.7314 Å on the right. The former is the wave-length of the
primary radiation.
نتائج تجربة كومبتون:
لقد وجد كومبتون أن الإشعاع المتبعثر له مركبتين؛ مركبة طولها الموجي
مساوٍ لطول موجة الإشعاع الساقط ومركبة أخرى تختلف في طولها الموجي
عن الطول الموجي للإشعاع الساقط وتعتمد على زاوية البعثرة وقد تمكن
كومبتون من شرح وجود مركبة الإشعاع المتبعثرة ذات الطول الموجي
المختلف عن الطول الموجي الساقط وذلك باعتبار الشعاع الساقط عبارة عن
حيث يعاني كل فوتون من تبعثر (تشتت) مرن hv شعاع من الفوتونات بطاقة
مع كل إلكترون. elastic scattering
momentum وكما هو معلوم، في حالة التشتت المرن فإن كمية الحركة
momentum and energy ( كميات تخضع لقانون الحفظ (البقاء energy والطاقة
.must be conserved
PDF created with pdfFactory Pro trial version www.pdffactory.com
- ١٩ -
ولتفسير هذه الظاهرة رياضياً، افترض كومبتون أن الفوتون له كمية
تعطي بالعلاقة p حركة
(1-9)
c
p= hv
حيث تم اعتبار الحركة الديناميكية للفوتون كجسيم يخضع لقوانين النظرية
النسبية والتي توضح العلاقة بين الطاقة وكمية الحركة.
[ ] 2 (1-10)
2 2 2 1
o E= (m c ) +(pc)
عند v للجسيم، وسرعة الجسيم rest mass هي الكتلة السكونية mo حيث
تعطى بالعلاقة p كمية الحركة
[ ] 2
2 2 2 1
ο (m c ) (pc)
dp
d
ap
v = aE = +
[ ] (pc)
ap
(m c ) (pc) d
2
1 2
1
2 2 2
ο
- = = +
[ ] (pc)c
(m c ) (pc)
1
2
1
2
2 2 + 2 1
=
°
(1-11)
2
2 4 2 2 1
2 2
(m c p C )
pc
E
v pc
+
\ = =
°
(1- في معادلة ( 11 v= c و m° = o في حالة الفوتون، نعوض عن
E pc (1-12)
E
C pc
2
\/ = Þ =
E = hv 1) حيث - 1) نتحصل على معادلة ( 9 - من معادلة ( 12
C
hv
C
p = E =
ساقط على p° دعنا نفترض الآن وجود فوتون بكمية حركة ابتدائية
أما p إلكترون ساكن. وبعد التصادم، نفترض أن كمية الحركة للفوتون
PDF created with pdfFactory Pro trial version www.pdffactory.com
- ٢٠ -
وبتطبيق قانون بقاء كمية .pe بكمية حركة recoil الإلكترون فيحدث له ارتداد
.(1- الحركة (انظر شكل 7
p p p (1-13) e = + °
بتربيع طرفي المعادلة.
p p p 2p p (1-14) 2 2
e
2 r r
° ° = - -
نطبق الآن قانون بقاء الطاقة
[ ] قبل التصادم 2 E أولاً، طاقة الإلكترون
E= (m c2 )2 + (pc)2 1 °
P لأن الإلكترون ساكن قبل التصادم (لأن أن m° = بالتعويض عن 0
تساوي صفر).
\E=m c=mc2 (1-15) °
قانون بقاء الطاقة: طاقة الإلكترون والفوتون الساقط قبل التصادم = طاقة
الإلكترون والفوتون بعد التصادم
2
2 2 1
e
hv +mc2 =hv +(m2 c4 +p c ) °
PDF created with pdfFactory Pro trial version www.pdffactory.com
- ٢١ -
للطرف الأيسر وتربيع طرفي المعادلة hv بنقل
2 2 2 4
2 2 2 2
e
2 4
2 2
e
2 2 2 4
(hν hv) 2mc (hv hv) m c
m c p c (hv hv mc )
or
(hv mc hv) (m c p c )
= - + - +
+ = - +
+ - = +
° °
°
°
(1-16)
c 1)، بالتعويض عن - من معادلة ( 14
hv
, p
c
p hv °
° = =
)cosθ
c
)(hv
c
hv
) 2(
c
) (hv
c
hv
p 2 ( 2 2
e
\ = ° + - °
هي الزاوية المحصورة بين اتجاه الشعاع المشتت والشعاع θ حيث
C الساقط. بضرب طرفي المعادلة في 2
p 2 c2 (hv )2 (hv)2 2(hv )(hv)cosθ (1-17)
e ° ° = + -
(1- لمعادلة ( 17 [2hv°hv] وللحصول على مربع كامل، نضيف ونطرح
14444244443 1444442444443
(hv hv)2 2hv hv (1 cos θ)
2 2 2 2 p c (hv ) (hv) 2hv hv 2(hv )(hv) 2(hv )(hv)cosθ
° -
° °
° -
° ° + - + - e
\p 2 c2 =(hv -hv)2 + 2hv hv (1- cosθ) (1-18) e ° °
1) نتحصل - 1) في معادلة ( 18 - من معادلة ( 18 (hv° -hv) بالتعويض عن قيمة 2
على
m2c4 +p 2c2 =p 2c2 -2hv hv (1- cosθ)+2mc2 (hv -hv) +m2c4 e e ° °
1-19 ).. بحذف الحدود المتشابهة من طرفي المعادلة: )
PDF created with pdfFactory Pro trial version www.pdffactory.com
- ٢٢ -
h(1 cosθ) mc (λ λ )
λ λ
λ λ
(1 cosθ) 2mc h
λ λ
2h c
or
λ λ
λ λ
(1 cosθ) 2mc h
λ
h c
λ
2h c
)
λ
1
λ
) 2mc hc ( 1
λ
c
λ
2mc h( c
2mc h (v v)
2hv hv (1 cosθ) 2mc (hv hv)
3
2
2
2
2 2
2
2
°
°
/ °
°
/
°
°
°
° °
°
° °
- = -
-
- / /
/ /
/ /
-
- =
= - -
= -
- = - -
(1 cosθ) ...(1-20)
cm
or λ - λ = h - °
mc لاحظ أن
1) له بعد الطول وهذا الحد يسمى طول - في معادلة ( 20 h
للالكترون ومقداره Compton wavelength موجة كومبتون
2.4 10 cm (1-21)
mc
h @ ´ -10
l وقد تبين من القياسات المعملية أن طول موجة الفوتون والمتشتت
(انظر شكل والذي l تتطابق مع القيمة النظرية. أ ما المركبة الثانية ل
) والتي لا l° والأخرى مساوية ل l° إحداهما تختلف عن l يبين مركبتين ل
تتغير بالنسبة فإن منشأها هو تصادم الفوتون الساقط مع الذرة ككل، فلو عوضنا
بكتلة الذرة (بدلاً من كتلة الإلكترون) وحيث أن هذه القيمة في المقام m عن
mc (وهي كبيرة جداً بالنسبة لكتلة الإلكترون) فإن الحد
ستكون قيمته صغيرة h
وأخيراً ما الذي l »l° وهذا يعني λ - λ° @ ο جداً قريبة من الصفر، أي أن
نستنتجه من تأثير كومبتون؟
إن القياسات التي أجريت على الإلكترون المرتد والفوتون المتبعثر منه
تؤكد- بما لا يدع مجالاً للشك – بأن هذا التصادم مماثل للتصادم الذي يحدث
PDF created with pdfFactory Pro trial version www.pdffactory.com
- ٢٣ -
بين كُرتي بلياردو، أي أن الفوتون (أو الشعاع الساقط) يجب أن تتعامل معه
على أساس أنه جسيم، وهذا يؤكد الطبيعة الجسيمية للإشعاع






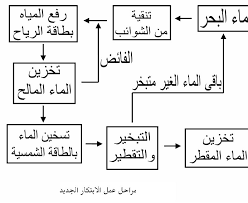
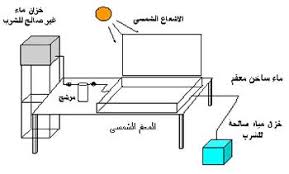





» انواع دايود الليزر
» ماهو الغشاء الرقيق؟
» حروف تدل على شخصية المراة ؟؟
» خاطرة ...!
» قصة .. توقف لسانه عن الكلام عندما علم أنها ابنة 17 سنة
» شاب يخاطب المساجد ...!!!! كم هو جميل ..؟؟!!!
» حدث في 25 سبتمبر
» حدث في 16 شوال